（一）DeepLearning (DL)概述

1. 什么是DL？

机器学习ML的框架：

(1)数据：\({(x_i,y_i)}, 1\le i \le m\)

(2)模型：\(\mathcal{F}={f(x;\theta)}, \theta\in\Theta\)

i. 线性： \(y=f(x)=w^Tx+b\) 【x——>y】

ii. 广义线性：\(y=f(x)=w^T\phi(x)+b\) 【x——>[\(\bar{x}=\phi(x)\)]——>y，其中的\(\phi\)为模式识别中的特征Feature，这一步也称为特征学习。】

iii. 非线性：人工神经网络（ANN）

(3)准则：损失函数\(L(y,f(x))\)

经验风险：\(R(\theta)=\frac{1}{m}\sum_{i=1}^m{L(y,f(x_i,\theta))}\)

正则化项：\(|w|_2^2\)

Minimizing： \(R(\theta)+\lambda|w|_2^2\)，或稀疏正则项L1.

因此转化为一个最优化问题。

神经网络ANN中 \(y=\sigma(\sum_i{w_i x_i+b})\) 相当于从P维到Q维的一个映射函数。则DL就是解决这个深度前馈神经网络的算法。

2. 存在的困难及挑战

可训练的参数太多；【参数过多带来的问题具体包括：计算资源要大，数据要多(否则出现过拟合)，算法效率要高】

多层网络以后的优化问题变为非凸优化问题；

梯度弥散问题，即从网络层由上往下的参数调节变得非常困难；

解释困难(可通过一些可视化的方法一定程度上来进行解释)；

3.算法历史

1958年，感知机Perception：一个神经细胞的处理能力较差，与或运算无法实现。

1986年，神经网络的概念出现：BP算法，对浅层网络做了很多的工作。一方面受限于当时的硬件和软件问题。

1998年，CNN卷积神经网络，在手写体识别中取得了成功。—LeCun

2006年，DBN深度置信网络，—Hinton

4.为什么学习DL

有效！【语音识别，目标识别，NLP，CV….】

5.领域概述

学术机构：

TorontoU，Hinton，1975年EdinburghU’s PHD;
NewYorkU，LeCun，1987年PHD;
MentrealU，Bengio，1991年McGillU’s PHD;
StanfordU, Ng，2003年UCBerkeley’s PHD;

学术会议：
NIPS，ICML，ICRL，…

参考: 深度学习课程-概述

（二）FNN & BP

一.前馈神经网络FNN

1.神经元、神经层、神经网

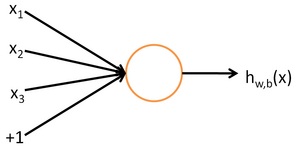
神经元
x_1 -w_1-\
..  -w_i--〇z--->a
x_p -w_p-/

一个神经元的输出是一个线性函数与一个非线性函数的复合：\([z=\sum w_ix_i+b,~a=f(z)]=>a=f(\sum w_ix_i+b)\).

其中激活函数包括：sigmod: \(\sigma(x)=\frac{1}{1+e^x};~\tan(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}};~|x|;~\)等

神经层
x_1 -w_1--〇--\-〇-->a_1 
              X
..  -w_i--〇--X-〇-->...
              X
x_p -w_p--〇--/-〇-->a_p

神经层上的每个神经元的输入时相同的，但权值是不同的。我们用 \( a^{(l)}_i \)表示第 \( l \)层第 \( i \)单元的激活值（输出值）。

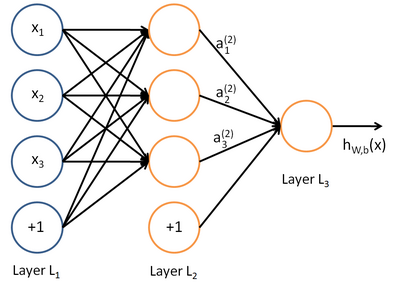
神经网
-〇-\    -〇-\
-〇--〇-/-〇--〇-...
-〇--〇-\-〇--〇-...
-〇-/    -〇-/
n_1  n_2  n_3   ...   n_L

2.记号

超参数(并不是学习出来的，而是认为根据需要设定的参数，也称元参数)：层数L，第l层的神经元个数\(n^{(l)}\)，神经元非线性函数\(f_l()\).

要学习的参数：连接权weight参数\(w_i^{(1)},w_i^{(2)},..w_i^{(L)}\)，两层之间的连接权。 偏bias参数\(b^{(1)},b^{(2)},..b^{(L)}\).

第l层神经元的状态\(z^{(l)},1\le l\le L\)；第l层神经元的激活activation：\(a^{(l)}\)

3.前馈计算

(1)基本公式

\(z^{(l+1)}=w^l a^l+b^l \)

\(a^l=f_l(z^l) \)

\(h_{w,b}(x)=a^{(l+1)}=f(z^{(l+1)})\)

(2)前馈计算(\(W=(w^1,…,w^l),b=(b^1,..,b^l)\))

\(l=1, a^l=x\)

计算步骤：\(a^1->z^2->a^2->…->z^L->a^L\)

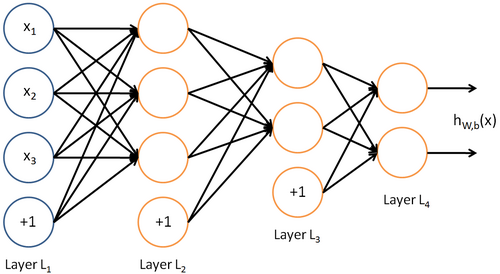
“目前为止，我们讨论了一种神经网络，我们也可以构建另一种结构的神经网络（这里结构指的是神经元之间的联接模式），也就是包含多个隐藏层的神经网络。最常见的一个例子是\(nl\)层的神经网络，第1层是输入层，第 \(n_l\)层是输出层，中间的每个层 \(l\)与层 \(l+1\)紧密相联。这种模式下，要计算神经网络的输出结果，我们可以按照之前描述的等式，按部就班，进行前向传播，逐一计算第 \(L_2\)层的所有激活值，然后是第 \(L_3\)层的激活值，以此类推，直到第 \(L{n_l}\)层。这是一个前馈神经网络的例子，因为这种联接图没有闭环或回路。”——UFLDL

4.应用于ML

数据D：\((x_i,y_i),1\le i\le N\)

模型M：\(y=h(x|w,b)\)

准则C: \(\sum_i|y_i-a^l(x|w,b)|^2+\lambda|w|_F^2) \)=min

其中，第二项是一个规则化项（也叫权重衰减项），其目的是减小权重的幅度，防止过度拟合: \(||w||F^2=\sum_i\sum_jw{ij}^2\)

权重衰减参数 \( \lambda \)用于控制公式中两项的相对重要性。

使用梯度下降法进行求解这个优化问题。

将上式写为：\(\sum_i J(x_i,y_i;w,b)+\lambda|w|_F^2\)=min

目标函数关于待求参数的导数：

其中：$$\frac{\partial|w|_F^2}{\partial w}=2w$$

然后重点求:$$\frac{\partial \sum J(.)}{\partial w};~~\frac{\partial \sum J(.)}{\partial b}$$

迭代公式：
$$w^{t+1}=w^t-\alpha \frac{\partial \sum J(.)}{\partial w}$$
$$b^{t+1}=b^t-\alpha \frac{\partial \sum J(.)}{\partial b}$$
其中\(\alpha\)是学习速率。

二.BP算法

“我们的目标是针对参数 \( W \)和 \( b \)来求其函数 \( J(W,b) \)的最小值。为了求解神经网络，我们需要将每一个参数 \( W^{(l)}{ij} \)和 \( b^{(l)}_i \)初始化为一个很小的、接近零的随机值（比如说，使用正态分布 \( {Normal}(0,\epsilon^2) \)生成的随机值，其中 \( \epsilon \)设置为 \( 0.01 \) ），之后对目标函数使用诸如批量梯度下降法的最优化算法。因为 \( J(W, b) \)是一个非凸函数，梯度下降法很可能会收敛到局部最优解；但是在实际应用中，梯度下降法通常能得到令人满意的结果。最后，需要再次强调的是，要将参数进行随机初始化，而不是全部置为 0。如果所有参数都用相同的值作为初始值，那么所有隐藏层单元最终会得到与输入值有关的、相同的函数（也就是说，对于所有 \( i\)，\( W^{(1)}{ij}\)都会取相同的值，那么对于任何输入 \( x \)都会有：\( a^{(2)}_1 = a^{(2)}_2 = a^{(2)}_3 = \ldots \)）。随机初始化的目的是使对称失效。”——UFLDL

1.多元函数的偏导数

(1)
$$X=[x_1,…,x_p]^T\in R^p,~ y=f(X)=f(x_1,…,x_p)$$
$$\nabla_x f(x)=\nabla_x y=\frac{\partial y}{\partial x}=[\frac{\partial f(x_1)}{\partial x},…,\frac{\partial f(x_p)}{\partial x}]^T\in R^p$$
(2)
$$x\in R^p, y=[..]^T\in R^q$$
$$y=[f_1(x),..,f_q(x)]^T$$
$$\nabla_xy=\nabla_x f(x)=\frac{\partial y}{\partial x}=[\frac{\partial f(x)}{\partial x_i}]^T\in R^{p\times q}$$
(3) 导数法则：链式法则

2.BP算法

BP思路：给定一个样例 \( (x,y)\)，我们首先进行“前向传导”运算，计算出网络中所有的激活值，包括 \( h_{W,b}(x) \)的输出值。之后，针对第 \( l \)层的每一个节点 \( i\)，我们计算出其“残差” \( \delta^{(l)}_i\)，该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点，我们可以直接算出网络产生的激活值与实际值之间的差距，我们将这个差距定义为 \( \delta^{(n_l)}_i \)（第 \( n_l \)层表示输出层）。对于隐藏单元我们如何处理呢？我们将基于节点（第 \( l+1 \)层节点）残差的加权平均值计算 \( \delta^{(l)}_i\)，这些节点以 \( a^{(l)}_i \)作为输入。

BP算法步骤：

(i)进行前馈传导计算，利用前向传导公式，得到 \( L2, L_3, \ldots \) 直到输出层 \( L{n_l} \)的激活值。

(ii)对于第 \( n_l \)层（输出层）的每个输出单元 \( i\)，我们根据以下公式计算残差：

$$\delta_i^{(n_l)}= \frac{\partial J}{\partial z_i^{n_l}}=-(y_i-a_i^{(n_l)})\cdot f’(z_i^{(n_l)})$$

(iii)令\(\delta^l=\frac{\partial J}{\partial z^l}\)，则对 \( l = n_l-1, n_l-2, n_l-3, \ldots, 2 \)的各个层，第 \( l \)层的第 \( i \)个节点的残差计算方法如下：（矩阵向量形式）

$$\begin{equation}\begin{split}\delta^{l}&=\frac{\partial J}{\partial z^{l}}=\frac{\partial a^l}{\partial z^l}\frac{\partial z^{l+1}}{\partial a^l}\frac{\partial J}{\partial z^{l+1}}\\
&=diag(f’(z^l))\cdot((w^l)^T\cdot\delta^{l+1})\\
&=(f’_l(z^l))\odot((w^l)^T\cdot\delta^{l+1})\\
&=((w^l)^T\cdot\delta^{l+1})\odot(f’_l(z^l))
\end{split}\end{equation}$$
以上逐次从后向前求导的过程即为“反向传导（BP）”的本意所在.

(iv)计算所需的偏导数：
$$\frac{\partial J}{\partial w^l}=\delta^{l+1}\cdot(a^l)^T$$
$$\frac{\partial J}{\partial b^l}=\delta^{l+1}$$

其中，假设 \( f(z) \)是sigmoid函数，并且我们已经在前向传导运算中得到了 \( a^{(l)}_i\)。那么，使用我们早先推导出的 \( f’(z)\)表达式，就可以计算得到 \( f’(z^{(l)}_i) = a^{(l)}_i (1- a^{(l)}_i)\)。

3.梯度下降法求解过程

(1) 对所有 \( l\)，令 \( \Delta W^{(l)} := 0 \), \( \Delta b^{(l)} := 0 \)（设置为全零矩阵或全零向量）

(2) For \( i = 1 \) to \( m\)，使用反向传播算法计算:

\(\nabla_{W^{(l)}} J(W,b;x,y) \)

\( \nabla_{b^{(l)}} J(W,b;x,y) \)

\( \Delta W^{(l)} := \Delta W^{(l)} + \nabla_{W^{(l)}} J(W,b;x,y) \)

\( \Delta b^{(l)} := \Delta b^{(l)} + \nabla_{b^{(l)}} J(W,b;x,y) \)

(3) 更新参数：
$$ \begin{align}
W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\
b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right]
\end{align}$$

重复梯度下降法的迭代步骤来减小代价函数 \( J(W,b)\) ，以训练我们的神经网络。